Autumn's Blog

Cuando empezaron mis vacaciones de verano una de las cosas que me propuse fue comenzar con el voice training, que consiste en una serie de ejercicios útiles para que las mujeres trans tengan una voz más femenina. Busqué tutoriales y cursos en Internet, y casi todo lo que encontré repetía la misma idea de que, como aspecto más básico, lo importante para cambiar la voz no es el tono, sino la resonancia.

Pero, ¿qué significa esto?

Tono vs resonancia

La gente comúnmente comete el error de asumir que la masculinidad o feminidad de una voz depende únicamente de su tono. El tono se refiere a qué tan aguda o grave es, cosa que en música y acústica se conoce como nota o altura. Muchas mujeres trans —y también muchos imitadores de voces novatos— suben su tono de voz lo más que pueden, y como resultado terminan sonando como Mickey Mouse o como Elmo. Incluso hay quienes utilizan la nariz para alcanzar un tono altísimo, haciendo así involuntariamente una voz como la de Cepillín.

Entonces la cosa no va realmente por ahí. A lo que verdaderamente se le debe prestar atención es a la resonancia. Cualquier persona que haya tomado clases de canto y locución (como yo, que mi padre me enseñó a cantar cuando era adolescente) ha escuchado sobre esto. Las cuerdas vocales producen el sonido, que recorre la laringe y la garganta y sale por nuestra boca. La resonancia de la voz tiene que ver directamente con la posición y el tamaño de la laringe, cosa que explicaremos más adelante.

Diagrama de una voz femenina y masculina. La laringe femenina está más hacia arriba y ocupa menos espacio, produciendo una voz más fina, mientras que la laringe masculina está más hacia abajo y ocupa más espacio, produciendo una voz más gruesa.

Podemos directamente modificar el tamaño y la posición de nuestra laringe, y ya habremos hecho la mitad del trabajo. Sin embargo, falta la parte que es menos intuitiva, pero que más efecto tiene.

Todo es una suma de senos

En 1821 —no mucho antes de que el Ejército Trigarante entrara en la Ciudad de México para firmar el acta de independencia con Juan O'Donojú— un reconocido matemático y físico francés llamado Joseph Fourier afirmó una barbaridad que dejó a todo el mundo perplejo: dijo que «cualquier onda, señal o función está construida con una suma de senos» [1] [2]. Sí, esa línea curva que constantemente iba hacia arriba y hacia abajo, y que tanto nos quebró el coco en la secundaria. Fourier se atrevió a desafiar todo lo que en ese momento se sabía, afirmando que podemos sumar la cantidad que queramos de senos, y así construiremos una onda o una señal cualquiera.

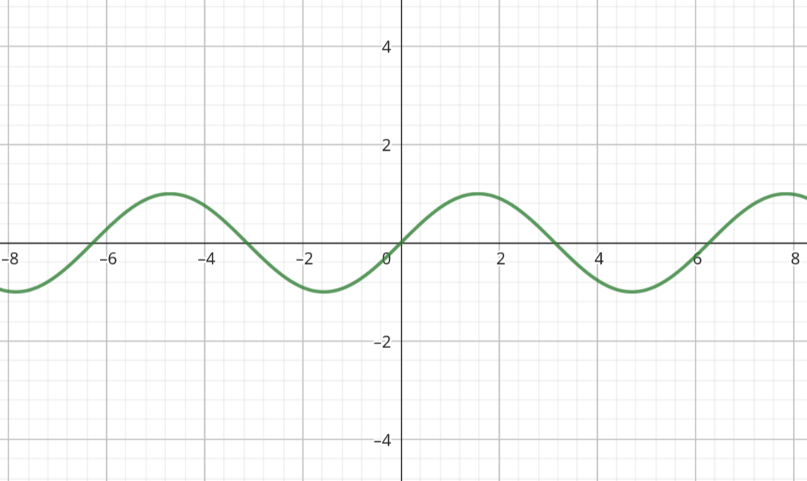
Una función seno sencillita, como las que veíamos en la secundaria. A saber, $f(x) = \sin(x)$

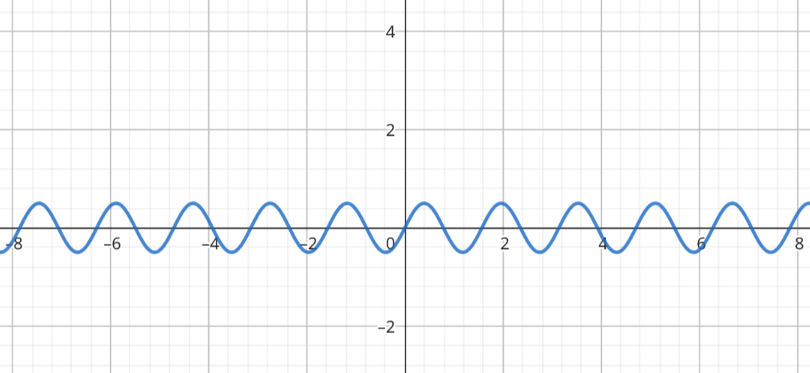
Otra función seno un poco más rebuscada. A saber, $g(x) = \frac{\sin(4x)}{2}$

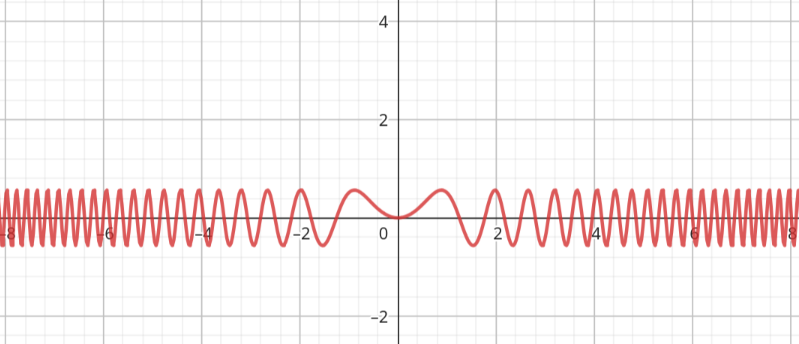
Otra función seno más complicada. A saber, $h(x) = \frac{\sin(2x^2)}{\sqrt{\pi}}$

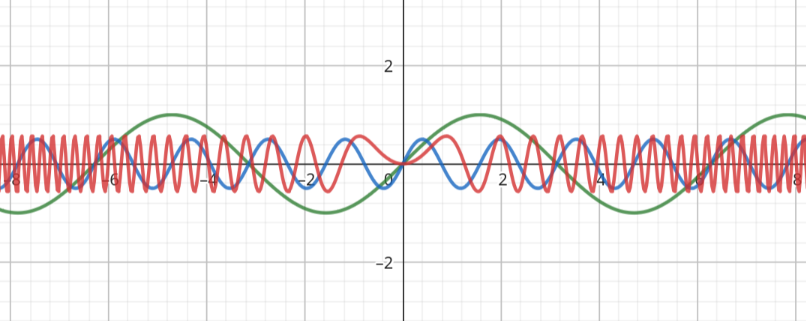
Las tres funciones superpuestas, que a simple vista no parecen tener relación ni sentido.

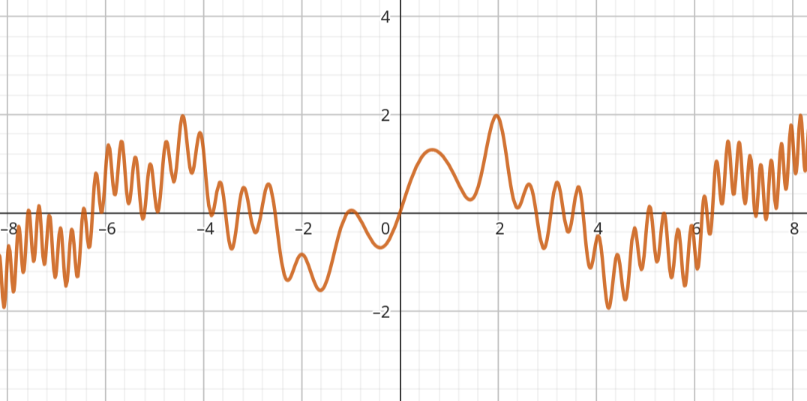
La suma de las tres funciones $f(x) + g(x) + h(x)$, que da como resultado esta barbaridad que no se parece en nada a un seno convencional.

No es necesario ser un genio en matemáticas para darse cuenta de como visualmente a partir de funciones seno sin relación aparente entre sí construimos una señal similar a las que se usan en el sonido y las telecomunicaciones. Tampoco hay que prestar atención a las fórmulas; las puse por si alguien quiere experimentar. Eso significa que nosotros podemos tomar una onda culaquiera —como por ejemplo, nuestra voz— y podemos descomponerla en un montón de funciones seno distintas.

La transformada de Fourier es una herramienta que nos permite justamente hacer eso; tomamos cualquier señal que queramos, y la descomponemos en un montón de funciones seno.

Conforme vamos sumando funciones seno distintas, la gráfica resultante se parece más y más a las líneas rectas.

Esta herramienta tiene una cantidad infinita de aplicaciones, y es en gran medida la base de las telecomunicaciones modernas. Sin embargo, la parte que nos interesa en esta entrada tiene que ver con el sonido, y particularmente la voz. Por ejemplo, veamos cómo se ve un acorde de Do Mayor tocado en un piano.

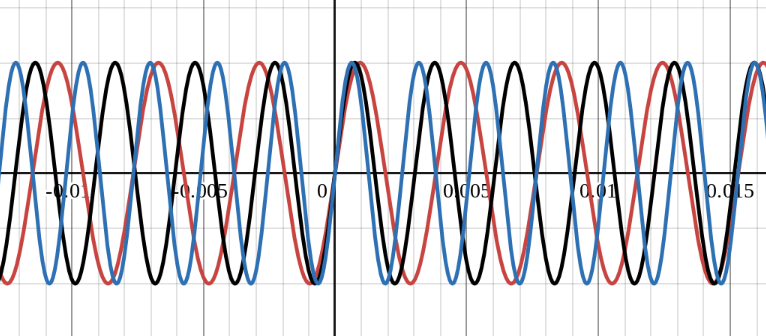
El acorde de Do Mayor expresado como funciones seno superpuestas.

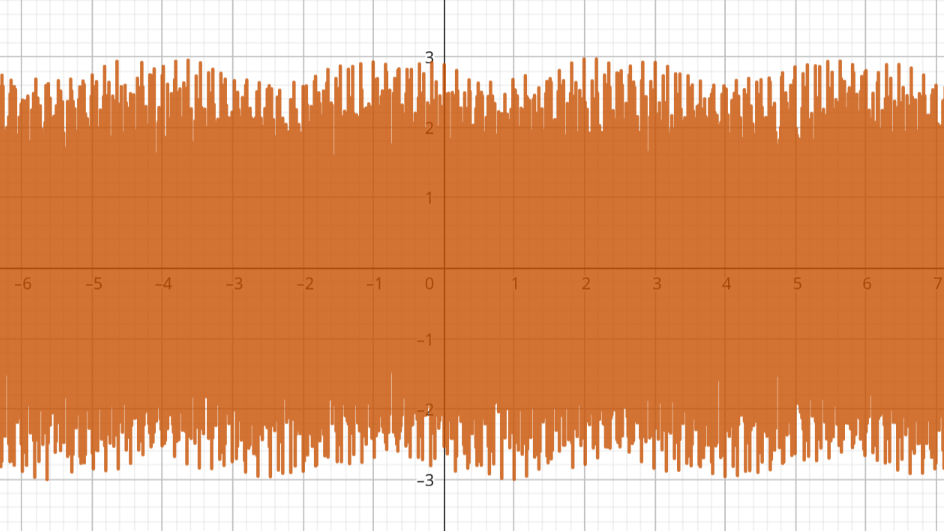
La suma de las funciones seno, dando como resultado esta brutalidad que sin embargo luce bastante regular, y que se parece mucho a las ondas que se suelen ver en programas como Audacity.

Ahora descompongámosla, y veamos con qué nos encontramos.

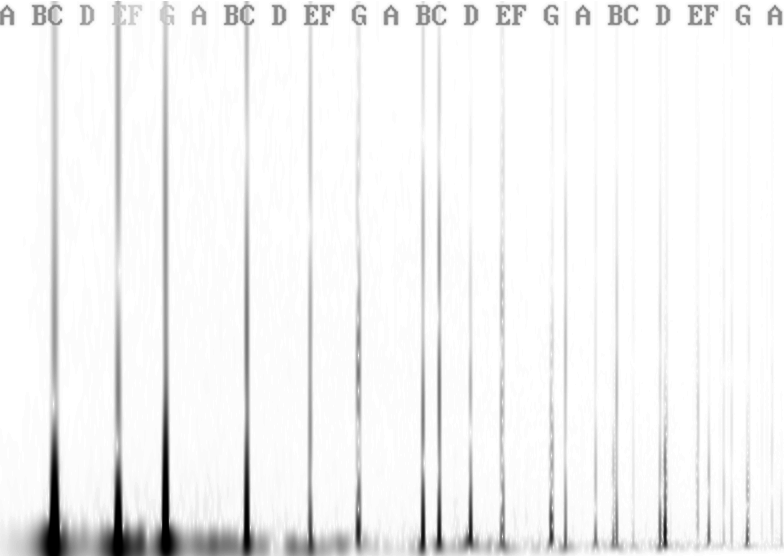
Transformada de Fourier del acorde. Las letras superiores son las notas en notación anglosajona. Las líneas más oscuras son los senos (es decir, las notas) más fuertes, volviéndose progresivamente más débiles.

Podemos ver las notas principales del acorde (Do-Mi-Sol) perfectamente representadas, pero luego resulta que estas mismas notas se empiezan a repetir a menor intensidad. Lo verdaderamente interesante de esto es que en un punto vemos a notas como Si, Re o hasta La sostenido representadas, siendo que estas notas no forman parte del acorde. Si ampliamos la transformada, podremos darnos cuenta de que, al final, todas las notas se involucran en el acorde; sólo que la mayoría son tan débiles que no las percibimos. La nota principal (en este caso Do) se denomina como fundamental, mientras que todas las demás notas se llaman armónicos. Toda señal tiene su fundamental y sus armónicos, siendo estos últimos el resto de funciones seno que se suman y le dan forma.

Todo esto nos dice que teóricamente podemos tener una fundamental y una cantidad infinita de armónicos, lo cual en teoría es cierto. Sin embargo, en la práctica los armónicos se vuelven cada vez más débiles, por lo que deberemos tomar una cantidad finita de éstos para incorporarlos a la señal, cosa que se denomina como ancho de banda (¡no te confundas con la velocidad de una conexión de red!); entre más ancho de banda, más armónicos se están tomando en cuenta, y la señal tiene una mejor calidad. Entonces, un sonido con un ancho de banda muy corto tendrá una calidad de teléfono debido a la poca cantidad de armónicos, mientras que uno con un ancho de banda muy amplio tendrá una calidad de estudio.

Hace unos días un gran amigo y hermano me contaba como se dio cuenta de que en una canción en MP3 no lograba percibir unos sonidos de ambientación que deberían escucharse de fondo, mientras que, con la misma canción en FLAC, sí que los escuchaba claramente. Eso es debido a que MP3 comprime el audio y, por ende, reduce el ancho de banda, eliminando entonces los armónicos de dichos sonidos ambientales, mientras que FLAC no comprime nada, por lo que todos los armónicos están disponibles.

Además, también podemos darnos cuenta de que una misma fundamental puede, de hecho, generar distintos armónicos, lo cual se conoce como resonancia. Entonces, la resonancia se refiere a la relación entre una fundamental con sus armónicos, que pueden ser (y son) distintos en cada caso. Es esta la razón por la que somos capaces de diferenciar el sonido de una guitarra y de un piano, incluso si ambos instrumentos tocan la misma nota; dado que los armónicos son diferentes, el sonido producido es distinto, y sin embargo no deja de ser coherente gracias a que la fundamental es la misma.

También, cuando utilizamos un ecualizador, lo que estamos haciendo es amplificar los armónicos del sonido que estamos reproduciendo, para así lograr darle una mejor calidad. ¿Alguna vez has visto este tipo de visualizadores?

Bueno, pues no es más que una representación hecha mediante la transformada de Fourier de los armónicos que suenan al reproducir una canción.

Los resonadores

Entonces, para conseguir una voz más femenina o más masculina, lo más importante que hay que hacer es cambiar la resonancia de nuestra voz. Esto lo podemos lograr alterando la altura y el espacio de nuestra laringe, como mencioné al principio. Esta entrada no es un tutorial de como hacer eso, pero pondré como ejemplo que, para levantar la laringe, podemos fingir que vamos a toser y fijarnos en la posición de nuestra garganta justo antes de hacerlo; para bajarla, podemos fingir que vamos a bostezar y fijarnos en la posición de nuestra garganta en el proceso.

Una laringe alta y que ocupa poco espacio producirá un sonido fino y suave, mientras que una laringe baja y que ocupa mucho espacio producirá el sonido opuesto. De este modo, al cambiar la resonancia de nuestra voz, estamos alterando su calidad sin necesidad de cambiar el tono.

También existe lo que en canto se conoce como “voz de pecho” y “voz de cabeza”, que en locución se llama “resonador de pecho” y “resonador de cabeza”, siendo ambas cosas lo mismo. Estos conceptos se refieren al lugar en donde la voz se amplifica, y donde adquiere mayor nitidez. Tampoco explicaré cómo usar ambos resonadores, pero aplicando los ejercicios de subir y bajar la laringe podemos hacernos una idea de cómo funciona. No es que literalmente la resonancia se dé en el pecho o en la cabeza; simplemente es que esas partes vibran con mayor fuerza como reflejo de nuestra voz. Si ponemos nuestra mano en el pecho y hablamos o cantamos, y éste vibra con fuerza, entonces estamos usando voz de pecho; si no vibra o vibra poco, estamos usando voz de cabeza.

Conclusión

Si bien es cierto que todo lo anteriormente mencionado juega un papel fundamental en la construcción de una voz, tampoco obtendremos mágicamente la voz deseada con tan sólo aplicar eso. Cosas como la entonación, los ademanes, el vocabulario y el “sentimiento” influyen muchísimo en la masculinidad o feminidad de una voz, que por supuesto se basa en estereotipos. Además, estamos hablando de un músculo, y como tal hay que entrenarlo.

Las primeras veces podría sonar muy forzado y podríamos terminar cansándonos, e incluso nos podría doler la garganta. Debemos practicar constantemente con el fin de acostumbrarnos a esa voz. El consumo de agua también es primordial, y también es preciso evitar el consumo de sustancias como el alcohol o el tabaco.

Esta ha sido una historia muy larga, y me ha tomado mucho tiempo estudiar —y sobre todo entender— todo esto. Aunque es cierto que las matemáticas no son necesarias para lograr cambiar nuestra voz, es innegable que gracias a ellas yo logré hacerlo.

Cuando los demás me preguntan sobre tips para cambiar la voz, no les suelo mencionar la parte matemática; les explico lo de la tos y el bostezo, y más cosas sencillas de aplicar para hacerse una idea de cómo funciona. Sin embargo, aquí quise sí mencionarla porque, además de que esto me enseñó que las matemáticas están en todo aunque no las percibamos, también me llevo el aprendizaje de que a veces una necesidad o un deseo nos puede llevar a lugares que nunca antes habíamos imaginado. ¡Sigamos aprendiendo, y sigamos compartiendo el conocimiento!