Autumn's Blog

Prólogo

Cualquier persona de la generación Millennial o anterior seguramente recordará bien todo el revuelo que causó la idea del llamado «efecto Y2K»: que a partir del año 2000 los sistemas informáticos de todo el mundo iban a fallar y «todo iba a colapsar», debido al incorrecto manejo de la fecha en las computadoras. Si bien no hubo ningún daño significativo a prácticamente nada —quedándose el Y2K entonces como una graciosa y ridícula anécdota de la paranoia que invadía las mentes de los mortales antes de la llegada del nuevo milenio— sí nos dejó imágenes curiosas como la siguiente.

Un letrero electrónico en la École centrale de Nantes, en Francia, que mostraba incorrectamente el año 1900 en vez del 3 de enero de 2000

El llamado «efecto Y2K38» (que tiene ese nombre porque ocurrirá en 2038) es relativamente similar a su antecesor, aunque las causas técnicas son totalmente distintas, y sus posibles consecuencias son más bien insignificantes, incluso hoy en día. Este es un tema que conocí cuando tenía 7 años gracias al video de Ridiculeando, y desde entonces me interesa muchísimo, por lo que me dedicaré en esta entrada a explicar todo con detalle, y a desmentir muchos de los mitos que rodean a esta situación.

Introducción: Unix Epoch 101

Para entender el problema del Y2K38, primero tenemos que ver la manera en la que las computadoras son capaces de calcular el tiempo. La implementación que nos interesa, que es la definida en el estándar POSIX, consiste en contar el número de segundos transcurridos (sin contar los intercalares) desde el 1 de enero de 1970 a las 00:00:00 hasta la fecha actual [1]. En cualquier sistema basado en Unix (incluyendo a GNU/Linux) se puede ejecutar el comando date +%s para obtener dicha información.

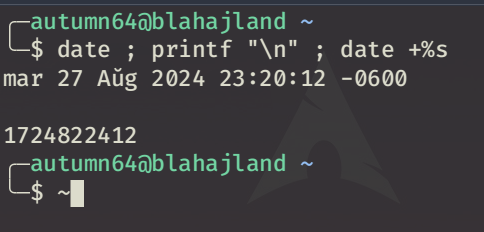
Captura de pantalla de mi distribución GNU/Linux, con un terminal mostrando la fecha y hora en la que ejecuté el comando, junto con su representación en segundos

A esto se le llama «tiempo Unix», en inglés “Unix Epoch”, y podemos convertir fácilmente cualquier fecha a TU, y viceversa. Si bien esto es más propio de los sistemas Unix-like, algunas aplicaciones para Windows también funcionarían de esa manera si fueron hechas en C.

Precisamente en C se utiliza algo llamado time_t, que sin saber programar podemos entenderlo como aquel elemento que está hecho específicamente para guardar y calcular el tiempo (y sabiendo programar, es básicamente el tipo de dato utilizado para tal propósito). Este time_t es un número entero con signo, y que tiene un tamaño predefinido. El hecho de que sea un entero con signo significa que, si guardamos valores negativos, la fecha será anterior a 1970, y si guardamos valores positivos, entonces la fecha será posterior.

Hice un pequeño programa en C demostrando el funcionamiento de time_t. Este es el código fuente:

// Unix Epoch a tiempo normal, por Mónica Gómez
#include <time.h>
#include <stdio.h>
#include <stdint.h>

int main(){
          time_t tiempo;
          printf("Introduce un número de segundos: ");
          scanf("%lld", &tiempo);
          printf("La fecha es %s\n", asctime(gmtime(&tiempo)));

          return 0;
}

Si nunca has programado, ¡no tengas miedo!, lo único relevante es la parte que dice time_t tiempo, que es en donde guardaré los segundos que introduzca en el scanf, y el segundo printf, que es en donde imprimiré la fecha convertida de TU a fecha normal.

Lo compilamos, y hacemos la prueba:

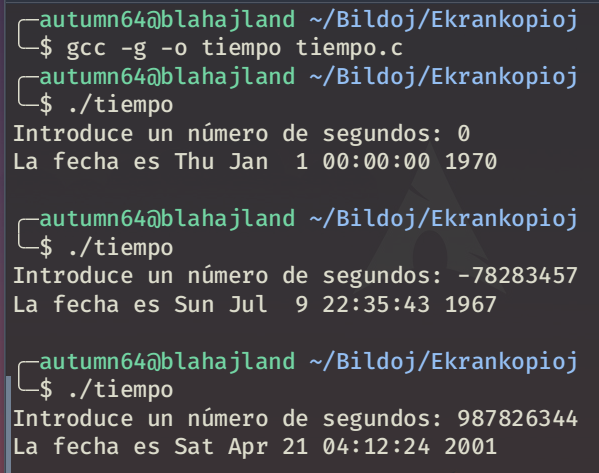
Demostración del funcionamiento del programa con un segundo cero, uno negativo, y uno positivo

Como podemos ver, cuando introduje el número cero, el programa mostró exactamente la fecha del 1 de enero de 1970 a las 00:00:00. Cuando puse un número negativo, el programa mostró una fecha anterior a 1970, en este caso 1967, y cuando puse uno positivo mostró una fecha posterior, en este caso 2001.

Entonces, este sistema es bastante transparente y sencillo para poder representar el tiempo en una computadora, por lo que se utiliza en todo lo que esté hecho en C, y en todo lo que sea basado en Unix (incluyendo a GNU/Linux y a Android). Como dato curioso, el 13 de febrero de 2009 a las 23:31:30 en horario UTC el TU fue 1234567890 [2].

¡Desbordemos un entero!

Cuando escribimos un número en nuestra computadora, ésta lo lee en formato binario. Sí, ese que es puros unos y ceros, y que a muchos nos quebró el coco en nuestra clase de informática de la preparatoria. Dado que los dos únicos dígitos disponibles son el 0 y el 1, para poder representar cualquier número mayor a esos dos toca repetirlos de forma posicional.

Piensa en el sistema decimal: tenemos los dígitos 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, y si queremos representar, por ejemplo, el número diez, entonces al 1 le ponemos un cero delante, y queda 10. Del mismo modo, si queremos representar el número cien, ahora le ponemos dos ceros delante, y queda 100. Estamos utilizando los mismos símbolos, pero el valor del dígito 1 cambia dependiendo de cuántos ceros tiene delante.

Exactamente lo mismo pasa en el sistema binario; para representar el número 2 ponemos 10, para el número 3 ponemos 11, para el número 4 ponemos 100, y así sucesivamente. Con esto, fácilmente podemos darnos cuenta de que un número relativamente pequeño ocupa de hecho demasiado espacio en binario, tanto que, por ejemplo, el número cien se representa en binario como 1100100. Un número de tres cifras en decimal se convirtió en uno de siete en binario.

Por esta razón, es común delimitar el tamaño máximo de cifras que puede tener un número en una aplicación, cosa que se denomina como «longitud», y que se mide en bits. Entonces, un entero (en este caso no tocaremos el tema del punto decimal, que se maneja de manera diferente) de 10 bits permitirá almacenar, como máximo, un número que en binario conste de 10 cifras. A saber, 1111111111, que vendría siendo el número decimal 1023. Entonces, nuestro entero de 10 cifras permite almacenar cualquier número entre 0 y 1023, dando un total de 1024 valores posibles.

Si quisiéramos forzar un número más grande, caeríamos en lo que se conoce como «desbordamiento de entero», que es clave para entender el tema del Y2K38. Si intentáramos meter uno más a nuestro entero, entonces el valor resultante sería 10000000000; el problema está en que ese es un número de 11 bits que no entra en nuestro entero de 10 bits, por lo que el primer 1 se descarta puesto que no cabe, y el número termina siendo 0000000000, o sea, cero.

El desbordamiento de entero es la explicación de muchos fenómenos populares relacionados con bugs. Por ejemplo, la Kill Screen de Pac-Man, en la que la mitad de la pantalla aparece toda glitcheada y que no permite avanzar de nivel, ocurre porque el contador de niveles del juego es de 8 bits, por lo que sólo permite almacenar valores de entre 0 y 255; un nivel después el contador se desborda y por eso ocurre el error. También es debido a un desbordamiento de entero que, cuando aprendíamos a calcular un factorial en nuestra clase de programación, después de un determinado número (si no mal recuerdo, el 31) el resultado daba 0, o alguna otra cosa aleatoria.

Los límites de time_t

La mayoría de computadoras domésticas del mundo eran de 32 bits cuando se hizo conocido el problema del Y2K38, lo que significa que time_t en esas computadoras tenía una longitud de 32 bits (excepto en GNU/Linux, cosa que veremos más adelante). Siguiendo la lógica de la sección anterior, podemos calcular fácilmente la cantidad de valores que podríamos meter en un entero de ese tamaño usando la fórmula $2^n$, en donde $n$ es el número de bits.

Si el tamaño de time_t es de 32 bits, entonces usamos la fórmula $2^{32} = 4 294 967 296$. Es decir, nuestro entero permite un poco más de cuatro mil doscientos noventa y cuatro millones de valores posibles.

¡Son un montón de números! Excepto por un pequeñísimo detalle. Si recuerdan, hace rato les dije que time_t es un entero con signo, lo que significa que tenemos que dividir ese número de la fórmula entre 2 y restarle uno, y entonces, si bien la cantidad de valores sigue siendo la misma, realmente el rango va desde -2 147 483 648 hasta 2 147 483 647. Para que me entiendan, si al principio podíamos contar desde el 1 de enero de 1970 a las 00:00:00 hasta cuatro mil millones de segundos adelante (que da una fecha de hasta el año 2106), resulta que debido al signo ahora sólo podremos hacerlo hasta dos mil millones de segundos (que llega hasta el 2038). De igual modo, si contamos hacia atrás, la fecha más antigua a la que podríamos llegar es al año 1901.

El efecto Y2K38

Habiendo dicho todo esto, resulta que el 19 de enero de 2038 a las 03:14:07 UTC el valor del contador de time_t llegará exactamente al valor 2 147 483 647. Un segundo después, ocurrirá el desbordamiento de entero, y el valor se regresará a cero o, peor aún, a -2 147 483 648. Entonces, las computadoras detectarán que están en 1901, lo que impedirá que los sistemas operativos y las aplicaciones funcionen correctamente.

Animación del efecto Y2K38

Esto es similar a lo que ocurrió con el efecto Y2K en el 2000, aunque en aquella ocasión la razón del problema fue mucho más sencilla. En el último cuarto del siglo XX los programadores tenían la costumbre de poner la fecha sólo mediante 2 dígitos, y escribían de antemano el 19. Entonces, si nosotros veíamos 1987, la computadora sólo veía el 87, y el 19 estaba puesto nada más como texto. Por eso, cuando llegó el nuevo milenio, la computadora no veía el número 2000, sino que veía el número 100, que se empalmaba con el 19, y a veces quedaba como 1900, y otras veces como 19100 [3].

La solución del Y2K fue relativamente sencilla —aunque se invirtieron millones de dólares en ella—, mientras que la del Y2K38 es mucho más complicada, si tomamos únicamente el punto de vista técnico. Programas como LibreOffice, el sistema de archivos, los navegadores web, e incluso RaccoonLock irían terriblemente mal o directamente no funcionarían debido al incorrecto cálculo de las fechas.

Si bien no se puede determinar con total certeza el impacto del problema, sí conocemos algunos de sus posibles efectos, de entre los cuales están los siguientes:

• Los dispositivos Android de 32 bits se bloquean y no se pueden ni reiniciar cuando llegan al límite del contador del tiempo.
• Cosas como los ABS de un automóvil, sistemas GPS, routers, y demás sistemas embebidos dejarán de funcionar.
• Algunos softwares de servidores, como AOLServer, no funcionarán correctamente.
• Imagina que en la noche del 18 de enero del 2038 vas a pedir un libro prestado, y al día siguiente en la mañana vas a devolverlo. El sistema, al haber cambiado bruscamente la fecha de 2038 a 1901, te cobraría como si hubieras tenido el libro prestado durante 137 años. Esto de hecho ocurrió en el 2000 en Pensilvania, Estados Unidos [4].
• Muchos videojuegos dejarán de funcionar debido a la incapacidad de calcular correctamente la fecha.

Que no panda el cúnico

Si recuerdan, hace rato les dije que este problema existe porque en la época en la que se hizo viral las computadoras eran de 32 bits y, por ende, time_t tenía ese tamaño. En 2024 la gran mayoría de computadoras y de smartphones son de 64 bits, y time_t tiene ahora ese nuevo tamaño. Si calculamos la cantidad máxima de segundos que podremos contar mediante la fórmula $2^{64}$, nos vamos a dar cuenta de que nos sale una cantidad agobiantemente grande, dando como límite unos 292 mil millones de años en el futuro. A manera de comparación, el universo tiene en este momento una edad de poco más de 13 mil 700 millones de años, por lo que haría falta que el universo tuviera 22 veces esa edad para alcanzar el límite.

En pocas palabras, es prácticamente imposible que a un usuario doméstico le ocurra eso, tomando en cuenta además que el 2038 será dentro de 14 años, y los sistemas de 64 bits se utilizan plenamente desde, más o menos, 2015. Solamente pueden resultar afectados sistemas como cajeros automáticos que sigan utilizando Windows XP y sistemas embebidos que para entonces ya tengan al menos 30 años. Es decir, si bien es muy interesante aprender sobre este problema, lo cierto es que el riesgo que supone es casi nulo.

Conclusión: Son unos capos los de GNU/Linux

Incluso si para el 2038 todavía hay quien utilice una computadora de 32 bits, sigue teniendo una manera extremadamente sencilla de resolver el problema, sin necesidad de cambiar a los 64 bits: instalar GNU/Linux. Esto es porque hace aproximadamente 8 años Linus Torvalds y el resto de contribuyentes del kernel se propusieron solucionar este problema. Se trata de algo mucho más técnico que no abordaré en esta entrada, por lo que dejaré este link para quien se interese en aprender sobre como hicieron para arreglarlo, aunque sí diré que, grosso modo, cambiaron la longitud de time_t de 32 a 64 bits, incluso si el sistema operativo en sí es de 32.

Entonces, independientemente de la computadora que tengamos para entonces, prácticamente no hay pierde si utilizamos GNU/Linux; es imposible que nos suceda el problema del Y2K38 gracias a la colaboracion de todas las personas que hicieron posible su solución. También es verdad que este problema puede ser diferente o no existir en sistemas operativos que no estén basados en el estándar POSIX (como Windows) o en aplicaciones que no hayan sido hechas en C o en lenguajes basados en éste (como C++ o Python).

En conclusión, pienso que este problema es súper interesante porque, a pesar de que al menos en mi caso es imposible que me suceda puesto que todos mis dispositivos son de 64 bits, sí que nos enseña un montón de cosas, y gracias a ello podemos comprender de una mejor manera como funcionan las computadoras.